はじめに
マーケティングの世界では、新たな手法や概念が次々と登場し、その中でも注目を集めているのが「負の二項分布」です。特に、森岡毅氏がこの概念を強く推奨していることから、多くのマーケティング責任者が関心を寄せています。本記事では、負の二項分布の基本概念から、森岡氏がなぜこの手法を推奨するのか、そして実際にマーケティング業務でどのように活用できるのかについて具体的に解説します。
森岡毅氏についてはこちらで解説していますので、ご覧ください。
負の二項分布とは?
負の二項分布は、確率論と統計学の分野でよく知られる概念で、マーケターの森岡毅氏が著書「確率思考の戦略論 USJでも実証された数学マーケティングの力」でも紹介しておりマーケティング、ビジネスの領域で有名な概念となっています。簡単に言うと、ある一定期間内に「ある行動(購入や利用など)」が何回起こるかを、集計単位(個人や世帯など)の全体分布として捉え、予測・分析するための統計モデルです。これを使うことで異なるカテゴリーの消費者の購買行動でも同じ法則にも基づいているということが表せます。
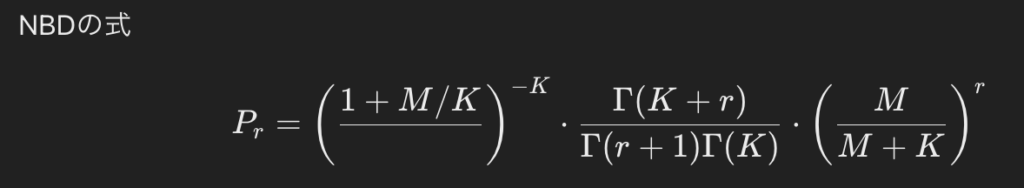
活用の目的
NBDモデル(Negative Binomial Distributionモデル)は、ある一定期間内に「ある行動(購入や利用など)」が何回起こるかを、集計単位(個人や世帯など)の全体分布として捉え、予測・分析するための統計モデルです。主に次のようなことができます。
購買・利用回数の分布予測
個々の消費者(世帯)が、その期間に何回購入(利用)するかという“回数分布”を推定し、全体としてどれくらいの割合の人が「0回」「1回」「2回」…というふうに分布するかを予測できます。
例)
| 購入回数 | 割合 | 人数 |
|---|---|---|
| 0回購入 | 80% | 80人 |
| 1回購入 | 10% | 10人 |
| 2回購入 | 4% | 4人 |
| 3回購入 | 3% | 3人 |
| 4回以上購入 | 2% | 2人 |
ブランドの利用構造・潜在市場把握
一定期間内に使う人・使わない人の割合や、ヘビーユーザーの比率などを把握し、ブランドの利用構造を理解するのに役立ちます。購買頻度が低い層を新たに取り込むべきか、ヘビーユーザーを維持すべきか、といった施策立案の参考になります。
売上やシェアの推定
回数分布がわかることで、顧客単価・購買回数の両面から売上や市場シェアをシミュレートしたり、施策の効果を予測したりできます。
類似データのモデリングや長期予測
購買だけでなく、本の貸し出し回数やサービス利用頻度など「ある行動回数」を扱うデータであれば、同様の手順でNBDを使い分布予測できます。過去データから将来の利用回数分布を推定し、在庫やサービス供給量の計画に応用することも可能です。
式の説明
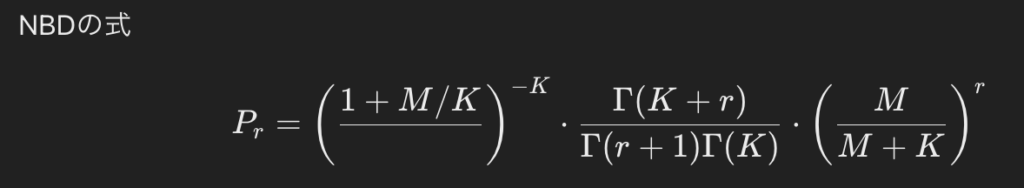
各パラメータの意味合い
- M:
- 該当カテゴリーや該当ブランドに対しての、一定期間での平均購入個数。
- 「1人(または1世帯)あたりの平均」がどれくらいかを示す指標。
- 著書では「自社ブランドを全ての消費者が選択した延べ回数(累計数)を、消費者の頭数で割ったもの」と説明
- K:
- 購買(行動)回数に対する「個人差の大きさ」を示すパラメータ。
- K が大きいほど「ばらつきが小さい」、小さいほど「ばらつきが大きい」と解釈できる。
- たとえば、購買頻度が人によって大きく異なる(ヘビー層とライト層の差が大きい)場合は K が小さくなりやすい。
- r:
- 購買(行動)回数そのもの(0回、1回、2回…)。
- P(r) は「r回購入・利用する人が全体に占める確率」を表す。※Pは確率(probability)を示す
各要素の解説
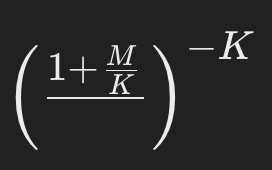
- 役割:分布のベース部分であり、分布全体の「正規化因子(スケール)」のような位置づけです。
- 「KとMの関係」によって、このベース部分の値が変わり、確率分布全体の大きさのバランスをとります。
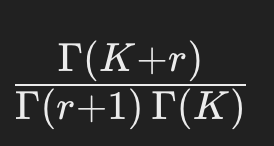
- 役割:“回数 r のパターン数”を加味する。ネガティブ・二項分布(NBD)の「組み合わせ係数」に相当します。
- r 回の事象が起こるパターンの数を表す要素、と考えるとイメージしやすいかもしれません。
- Γ関数:階乗を拡張した関数で、整数 nに対してはΓ(n)=(n−1)!になります。
- 「Γ(K+r)をΓ(r+1)Γ(K)で割った形」は、二項係数の一般化(K が整数でなくても使える形)としての役目を果たしています。
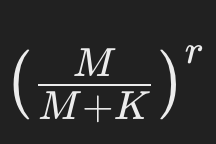
- 役割:“r 回発生する度合い”を反映。回数 r が増えるにつれて、どの程度確率が減少していくかを表す要素です。
- Mは「平均購買回数」、Kは「個人差のばらつき」のパラメータですが、両者の比率によって「回数が増えるほど確率がどんどん減る」という挙動を調整しています。
正直、数式を分解しても、数学が得意な人以外は何を言っているのかさっぱりな式ではないでしょうか笑
簡単に言うと、
- 期間内の平均購買数 M と、
- ばらつき指標 K
をもとに、
「回数が 0 回の人は全体の何%か」「1 回、2 回、…、多回数の人がそれぞれ全体の何%か」
を予測できるように設計された式だと思ってください。購買や利用の回数データを扱う際に頻繁に使われ、マーケティングでは「どのくらいの人が何回買うか」を知って戦略を立てるときに有用です。そこだけ理解いただければ、計算自体はExcelやAIに任せればOKです。
使い方の流れ
- MとKを特定
- まず自社実績データや市場全体のデータなどかMを特定します。
- 例)
- カテゴリーのMの場合:M=年間のカテゴリーの購入数/総ターゲット数
- 自社ブランドのMの場合:M=年間の自社ブランドの購入数/総ターゲット数
- 次にKを特定しますが、これはMがわかり、購入回数rを0の状態でNBDモデルの式に当てはめることで算出可能です。AIやExcelのソルバーという機能を使い、求めてみましょう。
- 回数分布の予測
- 算出したMとKを用いて、NBDモデルに当てはめ、0回・1回・2回…といった購買回数の分布を算出。
- マーケティングに活用
- 売上の予想:各回数の割合から人数、単価をかけて各回数ごとの売上を算出
- 改善施策の実行
- 水平方向の改善:0回の顧客を改善=新規顧客開拓
- 垂直方法の改善:1回以上の既存顧客の購入回数や人数を改善=既存顧客改善
要するに、NBDモデルはMの数値をもとに、将来や他条件下での“回数分布”を予測・分析する手法です。購買行動やサービス利用行動の全体構造を把握し、どの層にアプローチすべきかを考えるマーケティング施策に活用できます。
実績データと予想データの比較からわかる示唆
こちらの例は著書から引用した実例になります。パンケーキ、歯磨き粉、本の貸し出しのそれぞれの回数別の確率予測をNDBモデルで導き出し、実測データと比較しているデータです。
それぞれ「0回」「1回」「2回」…といった回数の利用者(購入者)が全体に占める割合を示しています。実測と予測を比べると、多くの項目でほぼ同様の割合が得られており、NBDモデルが実測データを比較的よく捉えていることがわかります。
| 回数 | (1) パンケーキ2週間 1000世帯 | (2) 歯磨き粉の購入四半期 5240世帯 | (3) 本の貸し出し1年間 9480冊 |
|---|---|---|---|
| M | 0.736 | 1.46 | 0.993 |
| K | 0.6016 | 0.78 | 0.475 |
| - | 実測 / 予測 | 実測 / 予測 | 実測 / 予測 |
| 0回 | 62% / 62% | 44% / 44% | 58% / 58% |
| 1回 | 20% / 21% | 19% / 22% | 20% / 19% |
| 2回 | 4% / 4% | 14% / 13% | 9% / 9% |
| 3回 | 4% / 4% | 9% / 9% | 5% / 5% |
| 4回 | 1% / 1% | 3% / 2% | 3% / 2% |
| 5回 | 1% / 1% | 3% / 2% | 2% / 2% |
| 6回以上 | 8% / 7% | 8% / 8% | 3% / 3% |
| 合計 | 100% / 100% | 100% / 100% | 100% / 100% |
カテゴリー(製品・サービス)の性質による差
- (1)パンケーキ(2週間・1000世帯):
- 0回利用が6割以上と多く、「買わない/作らない世帯」が大半を占めている。
- ヘビーユーザー(6回以上)は全体の1割弱ほど。
- (2)歯磨き粉の購入(四半期・5240世帯):
- 平均回数1.46回とやや高めで、2回や3回購入者の割合もそこそこ多い。
- “生活必需品”として定期的に買う層があると推測できる。
- (3)本の貸し出し(1年間・9480冊):
- 0回(全く借りない)が約6割。1回~3回程度が多く、6回以上のヘビーユーザーはわずか3%。
- 「全く利用しない層がかなり多い」「少数だが頻繁に利用する層がいる」という利用構造がうかがえます。
NBDモデルを用いた回数予測の意義
- 平均回数 M と ばらつきパラメータ K によって、観察期間内で「何回利用する人がどのくらいの割合で存在するか」を推計できます。
- たとえば、(2)歯磨き粉のM=1.46は、(1)パンケーキ( M=0.736 )よりも使用頻度が高いことを示しています。さらにKの値を合わせてみると、「利用頻度における個人差の大きさ・小ささ」が把握できます。
- (2)歯磨き粉: K=0.78 ⇒ 比較的ばらつきが小さい(多くの人がそれなりの頻度で買う)。
- (3)本の貸し出し: K=0.475 ⇒ 個人差(ヘビーとライトの差)が大きい。
マーケティング・施策への応用
- 「0回」の層が多ければ「まず試してもらう/使い始めてもらう」プロモーションに注力する。
- 「頻度が高い層」をどのくらい重視し、囲い込み施策を行うか。
- 製品別・サービス別に、施策ターゲットを定めるうえで参考になるデータです。
- NBDモデルは「一定期間内に起こる行動回数の分布」を説明・予測する際に広く用いられる。
小学生でもわかる負の二項分布を使い所
アイスクリーム屋さんを例にして、負の二項分布(NBD)を小学生向けにやさしく説明してみます。
アイスクリーム屋さんの「来店回数」をイメージ
友達が1か月のあいだに、「アイスクリーム屋さんに何回行くか」を考えてみましょう。
- Aくんは大のアイス好きで毎日のように行きます。
- Bちゃんはアイスは好きだけれど週に1回くらい行きます。
- Cくんはあまり行かないか、行っても月に1回くらい。
- Dさんはダイエット中で、この1か月は1回も行かない。
いろんな子や大人がいて、「アイスを買いに行く回数」は人によってバラバラですよね。
「みんな合わせると、何回行く人がどのくらいいるか?」を知りたい
お店の人は、こんなことを知りたいとします。
- 「0回(全く来ない)人は、全体のどれくらいいるの?」
- 「1回だけ来る人は何人くらいいるの?」
- 「5回以上来るヘビーユーザーはどれくらい?」
それを予測できると、アイスの材料を仕入れる量や、お店で働くアルバイトの人数を調整しやすくなります。
そこで登場!負の二項分布(NBD)
「負の二項分布(NBD)」は、
- みんなの平均的な来店回数(たとえば月に平均2回行く、という感じ)
- 人によってどれだけ回数の差があるか(すごくたくさん来る人と、ほとんど来ない人の差が大きいか、小さいか)
この2つの情報をもとに、「0回の人」「1回の人」「2回の人」…という回数ごとの人数(または割合)を計算するための“特別な数式”だと思ってください。
どうやって考えるの?
- 平均回数(M)
- みんなを全部合わせて平均したとき、1か月でどのくらいの回数行っているか。
- たとえば「平均2回くらい行っている」というのを M=2 みたいに表す。
- ばらつきパラメータ(K)
- 「アイスがすごく好きな人」と「あまり行かない人」の差がどれだけ大きいかを表す数字。
- 差が大きいほど K は小さく、みんなだいたい同じくらい行くと差が小さいので K が大きくなる。(回数0回の人の場合でKを計算するとK=2になる)
- 「何回行く人がどれくらい?」を予測する
- この2つの数字(平均回数 M とばらつき K)を入れると、
- 「0回の人は全体の何%」「1回の人は何%」「2回の人は何%」…という予測が出せる。
| 一ヶ月で アイスクリーム屋 にいく回数(r) | 割合 |
|---|---|
| 0 | 25% |
| 1 | 25% |
| 2 | 19% |
| 3 | 13% |
| 4 | 8% |
| 5 | 5% |
| 6回以上 | 6% |
- 0回が25%: 全く行かない(購入しない)層
- 1回が25%: 月に1回は必ず行く層
- 2回以上: 約半数(残りの約50%)
特に、2回~5回あたりにある程度のボリュームがあり、6回以上(ヘビーユーザー)は6% と少数ですが、一定は存在していることになります。ここから調査人数を掛け合わせていけば人数がわかり、そこに平均単価をかければ売上も見えてきます。
こんなふうに役立つ
- お店の準備
0回の人(来ない人)がすごく多いなら、「新商品のチラシを配って、まず1回でも来てもらおう」と考えられます。 - ファンを増やす施策
たくさん来る人(ヘビーユーザー)がある程度いるなら、その人たちにポイントカードを作ってもらうとか、イベントを開くとか、“もっと来てもらう工夫”を考えられます。 - キャンペーンの効果を予想
「もしクーポンを配ったら、月に1回だけ来ていた人が2回行くようになるかな?」など、新しいイベントやセールをした場合に、全体で何回くらい来店回数が増えそうかを予想できます。
まとめると、負の二項分布(NBD)は、「みんなが何回アイスを買いにくるか」をまとまった形で予想するための道具と言えます。「平均的に月に何回くらい行くか(M)」と「人によってどれくらい行き方がバラバラか(KK)」を使って、0回の人、1回の人、2回の人…という割合を計算します。
こうして「どのくらいの人がどれだけアイスを買う(食べる)のか」をざっくり見通せれば、お店の人はアイスを作る量やお店の企画を考えるときに、とても助かるわけです。
ポイントは、「来店回数のばらつきを含めて、全体としてどんなふうに分かれるか予測できる」 ところ。
アイスクリーム屋さん以外にも、お菓子やパンの購入回数、図書館の本を借りる回数など、「ある行動が、みんなそれぞれ月に何回ぐらい起こるの?」という場面で同じ考え方が使えます。
森岡毅氏が負の二項分布を勧める理由
森岡毅氏は、ユニバーサル・スタジオ・ジャパン(USJ)のV字回復を成し遂げたマーケティングの達人として知られています。彼が負の二項分布を推奨する理由は以下の通りです。
| 理由 | 詳細 |
|---|---|
| 予測精度の向上 | 顧客行動を精緻に予測できるため、投資が失敗せず、マーケティングキャンペーンの効果を最大化できます。 |
| リソースの最適配分 | どの顧客セグメントに対してどのようなマーケティング施策を展開すべきかを明確にできるため、リソースを効率的に配分できます。 |
| 効果的なターゲティング | 高価値顧客を特定し、より効果的なターゲティングが可能になります。 |
| 長期的な顧客価値の予測 | 顧客の生涯価値(LTV)をより正確に予測できるため、長期的な戦略立案が可能になります。 |
| キャンペーン効果の精密な測定 | 各マーケティングキャンペーンが顧客行動にどのような影響を与えたかを定量的に評価できます。 |
負の二項分布の実践ステップ
負の二項分布をマーケティングに活用するための具体的なステップを以下に示します。
| ステップ | 内容 | 具体的なアクション |
|---|---|---|
| 1. データの収集と整理 | 顧客データ(購入履歴、キャンペーン参加履歴、ウェブサイト行動データ)の収集。これらのデータからM(とK)を特定する必要があります。 | ・CRMシステムからデータを抽出 ・データクレンジングを実施 ・必要に応じてデータの統合 |
| 2. 分布のフィッティング | データを基に負の二項分布をフィッティング | ・統計ソフトウェア(R, Python等)を使用 ・最尤推定法でパラメータを推定 |
| 4. インサイトの抽出 | モデルから得られたパラメータを基に顧客行動のインサイトを抽出 | ・顧客セグメントごとの購買傾向を分析 ・次回購入までの期間を予測 |
| 5. マーケティング施策の立案と実行 | 高頻度で購入する顧客に対するロイヤリティプログラムなどの具体的施策を立案 | ・セグメント別のキャンペーンを設計 ・パーソナライズされたオファーを作成 |
負の二項分布を使ったマーケティング事例
事例1:ユニバーサル・スタジオ・ジャパン(USJ)
USJでは、来園者のデータを基に負の二項分布をフィッティングし、来園頻度や次回来園までの期間を予測しました。
| 施策 | 詳細 |
|---|---|
| セグメント別キャンペーン | 高頻度来園者向けの年間パスポート割引 |
| タイミングを考慮したプロモーション | 次回来園予測時期に合わせたメール配信 |
| 新アトラクション告知 | 来園頻度に応じたカスタマイズド告知 |
これらの施策により、USJは見事なV字回復を実現しました。
事例2:サブスクリプションサービスのチャーン予測
ある音楽ストリーミングサービスが、負の二項分布を使用して顧客のチャーン(解約)を予測した事例です。
| ステップ | 詳細 |
|---|---|
| データ分析 | 過去の利用頻度と解約率の関係を分析 |
| モデル構築 | 負の二項分布を使用してチャーン確率をモデル化 |
| 施策実施 | 高リスクユーザーに対するリテンション施策 |
具体的な施策例:
- 低利用頻度ユーザーへのパーソナライズドプレイリスト提案
- 利用頻度に応じた特別割引の提供
- 好みのアーティストの新曲リリース時の通知最適化
負の二項分布をマーケティングに活用するためのポイント
| ポイント | 詳細 | 実践方法 |
|---|---|---|
| データの質を確保する | 正確で詳細な顧客データを収集し、適切に整理する | ・データクレンジングの徹底 ・欠損値の適切な処理 ・異常値の検出と対処 |
| 統計的スキルを磨く | 負の二項分布を正しくフィッティングし評価するための知識とスキルを習得する | ・統計学の基礎学習 ・R, Pythonなどの統計解析ツールの習得 ・実データでの練習 |
| 継続的なモデルの更新 | 顧客行動の変化に合わせてモデルを定期的に更新する | ・定期的なデータ更新とモデル再構築 ・パラメータの変化トレンド分析 ・モデルのパフォーマンス監視 |
| 顧客セグメンテーションの精緻化 | モデルから得られたインサイトを基に、顧客セグメントを詳細に分ける | ・多次元でのセグメンテーション ・セグメント間の移動分析 ・セグメント別の施策効果測定 |
| ビジネスコンテキストとの統合 | 統計モデルの結果をビジネスの文脈で解釈し、実践的な施策に落とし込む | ・経営陣への分かりやすい報告 ・他部門との連携強化 ・ROIを考慮した施策立案 |
負の二項分布のメリットとデメリット
| メリット | デメリット |
|---|---|
| 高い予測精度 | 統計的知識が必要 |
| リソースの最適配分が可能 | データの質に依存 |
| 効果的なターゲティングが可能 | モデルの継続的な更新が必要 |
| 長期的な顧客価値の予測が可能 | 初期導入コストが高い |
| キャンペーン効果の精密な測定 | 解釈に専門知識が必要 |
まとめ
負の二項分布は、顧客行動を予測し、効果的なマーケティング施策を立案するための強力なツールです。森岡毅氏がこの手法を強く推奨する理由は、その高い予測精度とリソースの最適配分にあります。実際に負の二項分布を活用することで、マーケティングの効果を最大化し、競争力を高めることが可能です。
ただし、この手法を効果的に活用するためには、統計的知識とスキル、質の高いデータ、そして継続的な更新と改善が必要です。これらの課題を克服し、負の二項分布を戦略的に活用することで、マーケティング施策の精度と効果を大幅に向上させることができます。
マーケティング責任者として、この手法を理解し実践することで、さらなるビジネス成長を目指しましょう。負の二項分布は、データドリブンマーケティングの強力なツールとして、今後ますます重要性を増していくことでしょう。